堆排序
2024年04月03日
一、认识
堆排序HeapSort, 是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序实现分为两种方法:
大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列
小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列
二、特点
非稳定排序: 如果 a 原本在 b 的前面,且 a == b,排序之后 a 可能不在 b 的前面,则为非稳定排序。
原地排序: 原地排序就是指在排序过程中不申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。
排序方式: In-place (不占用额外内存,只占用常数内存)
时间复杂度: O(NLogN),这里 N 是数组的长度;
空间复杂度: O(1)
扩展: 排序算法的稳定性如下
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i] = r[j],且 r[i] 在 r[j] 之前,而在排序后的序列中,r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的。
那么排序算法的稳定性有什么意义呢?其实它只在一种情况下有意义:当要排序的内容是一个对象的多个属性,且其原本的顺序存在意义时,如果我们需要在二次排序后保持原有排序的意义,就需要使用到稳定性的算法。
三、思路
-
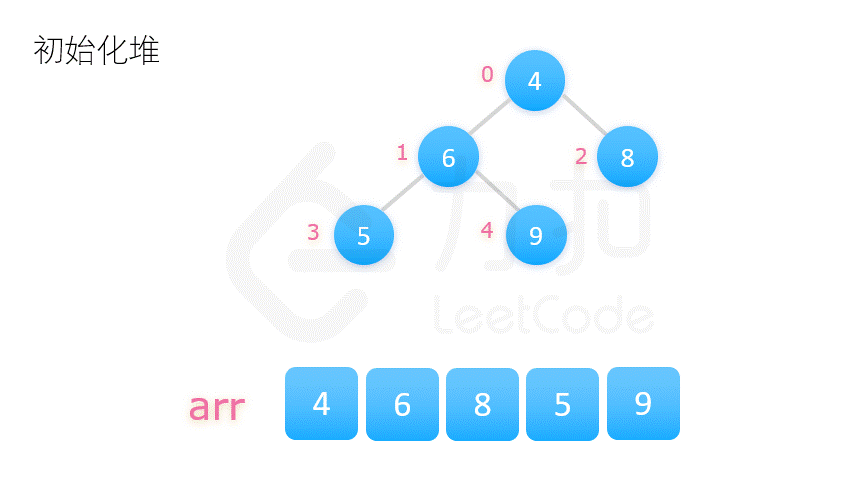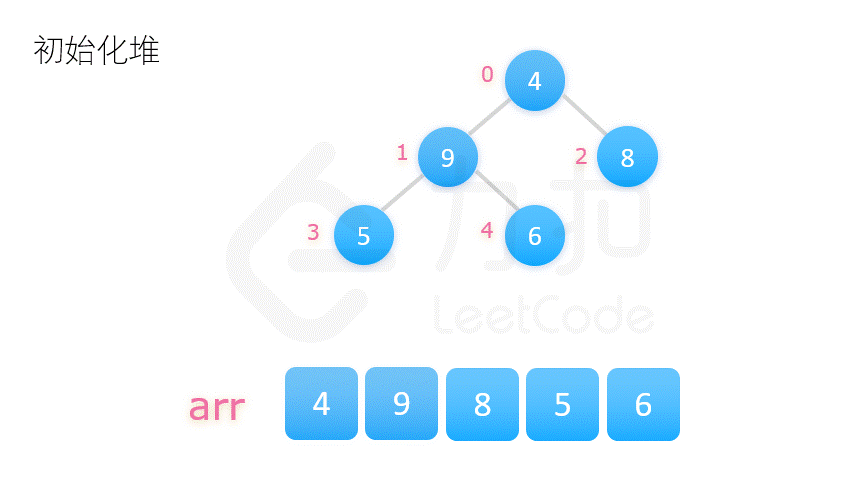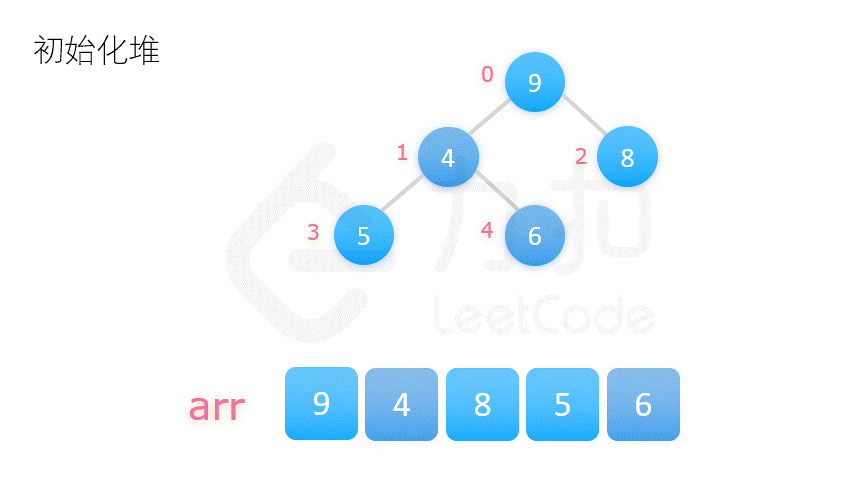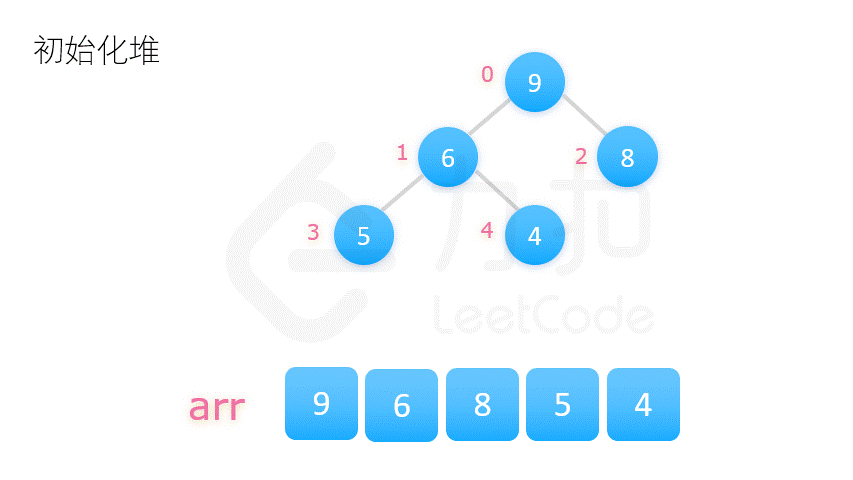
构建大顶堆: 从数组中心元素直到起始元素, 依次调整当前节点到堆底。
-
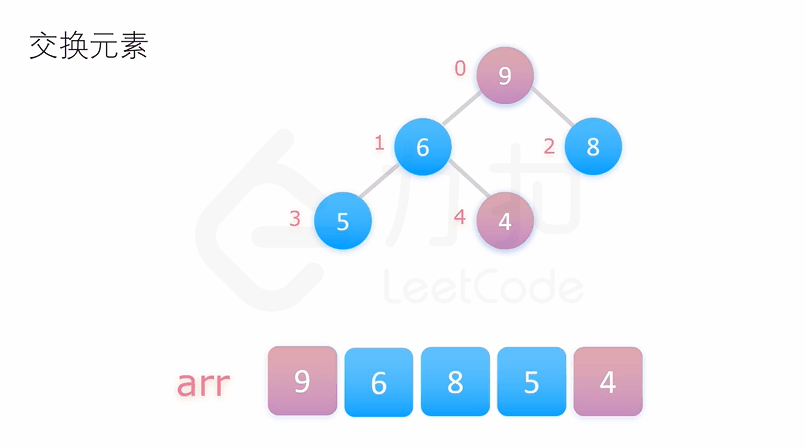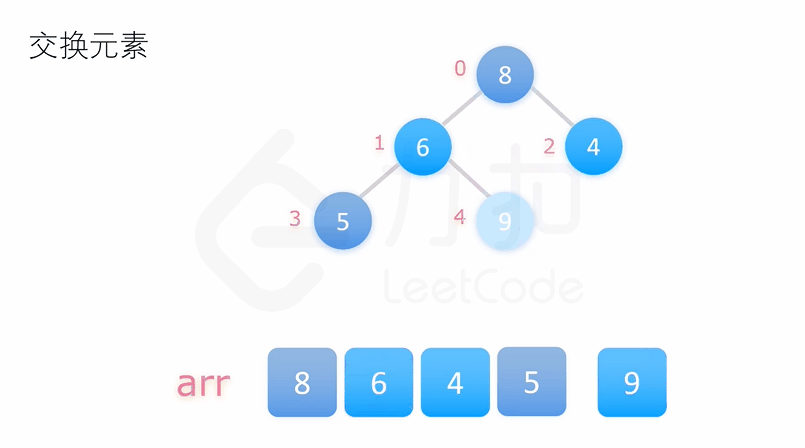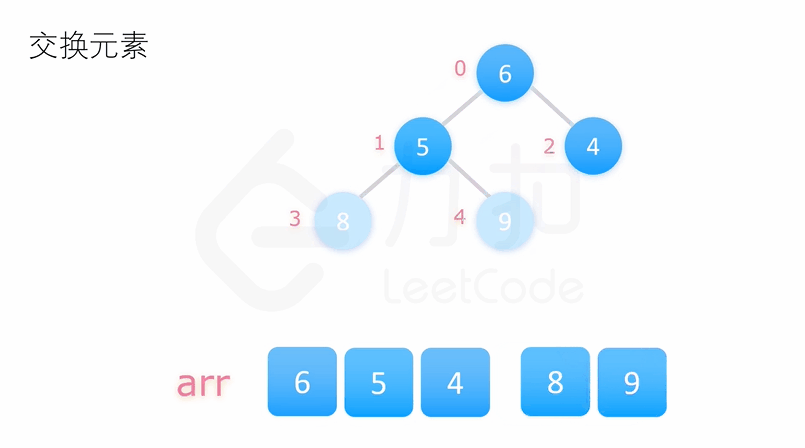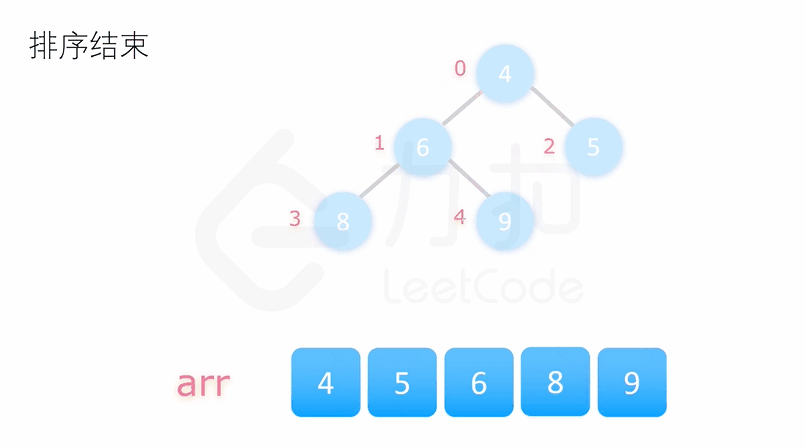
交换末尾元素与堆顶元素, 调整堆顶元素至当前元素
重复执行以上操作我们即能得到一个有序的序列
Preview
Preview
四、实现
function sort(nums) {
heapSort(nums);
return nums;
}
function heapSort(nums) {
// 将 nums 数组构建为大顶堆
buildHeap(nums);
// 从最后一个元素开始, 依次与堆顶元素进行交换, 然后重新调整堆
for (let i = nums.length - 1; i > 0; i--) {
[nums[0], nums[i]] = [nums[i], nums[0]];
shiftDown(nums, 0, i);
}
}
function buildHeap(nums) {
const halfLength = nums.length >>> 1;
for (let i = halfLength - 1; i >= 0; i--) {
shiftDown(nums, i, nums.length);
}
}
function shiftDown(nums, startIndex, endIndex) {
let i = startIndex;
const halfLength = endIndex >>> 1;
while (i < halfLength) {
const leftIndex = 2 * i + 1;
const left = nums[leftIndex];
const rightIndex = leftIndex + 1;
const right = nums[rightIndex];
if (left > nums[i]) {
if (rightIndex < endIndex && right > left) {
[nums[i], nums[rightIndex]] = [nums[rightIndex], nums[i]];
i = rightIndex;
} else {
[nums[i], nums[leftIndex]] = [nums[leftIndex], nums[i]];
i = leftIndex;
}
} else if (rightIndex < endIndex && right > nums[i]) {
[nums[i], nums[rightIndex]] = [nums[rightIndex], nums[i]];
i = rightIndex;
} else {
return;
}
}
}
测试
const nums = [1, 3, 6, 10, 8, 12, 7, 4, 5, 9, 2];
console.log(sort(nums));